
Categorisation of point groups by symmetry operations


|
Categorisation of point groups by symmetry operations |

|
This table lists point group symmetries along with their symmetry
operations, the order of the group (i.e. the number of symmetry
operations) and common notations.  links to a correlation table, and
links to a correlation table, and  links to tables of products of irreducible
representations. The group produced by combination with inversion is
listed under "x i". This, in the case of crystolographic point
groups, is the Laue class which corresponds to the symmetry
of reciprocal space. Isomorphic groups are also listed where
character tables are available.
links to tables of products of irreducible
representations. The group produced by combination with inversion is
listed under "x i". This, in the case of crystolographic point
groups, is the Laue class which corresponds to the symmetry
of reciprocal space. Isomorphic groups are also listed where
character tables are available.
| Operations | Order | Schönflies Symbol |
International Symbol |
Full Symmetry Symbol |
Correlation Table |
Irred. Rep. products |
x i | Isomorph. with |
| Cubic | ||||||||
| E, 4C3, 4C32, 3C2 | 12 | T | 23 | 23 |  |
Th | ||
E, 8C3, 3C2, 3 v,
i, 8S6 v,
i, 8S6 |
24 | Th | m3 | 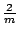 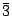 |
 |
Th | ||
| E, 6C4, 8C3, 3C2, 6C2' | 24 | O | 432 | 432 |  |
Oh | Td | |
E, 8C3, 3C2, 6S4, 6 d d |
24 | Td | 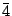 3m 3m |
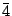 3m 3m |
 |
 |
Oh | O |
E, 8C3, 6C2, 6C4, 3C2',
i, 6S4, 8S6, 3 h, 6 h, 6 d d |
48 | Oh | m3m | 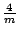 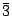 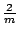 |
 |
 |
Oh | |
| Tetragonal | ||||||||
| E, C4, C2, C43 | 4 | C4 | 4 | 4 |  |
C4h | S4 | |
| E, S4, C2, S43 | 4 | S4 | 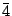 |
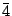 |
 |
 |
C4h | C4 |
E, C4, C2, C43, i, S43,  h,
S4 h,
S4 |
8 | C4h | 4/m | 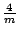 |
 |
 |
C4h | |
| E, 2C4, C2, 2C2', 2C2'' | 8 | D4 | 422 | 422 |  |
D4h | C4v, D2d | |
E,
2C4, C2, 2 v,
2 v,
2 d d |
8 | C4v | 4mm | 4mm |  |
 |
D4h | D4, D2d |
E, 2S4, C2, 2C2',
2 d d |
8 | D2d (Vd) | 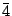 2m 2m |
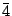 2m 2m |
 |
 |
D4h | D4, C4v |
E, 2C4, C2, 2C2', 2C2'',
i, 2S4,  h,
2 h,
2 v,
2 v,
2 d d
|
16 | D4h | 4/mmm |
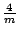 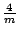 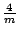
|
 |
 |
D4h | Orthorhombic |
| E, C2, C2', C2'' | 4 | D2 (V) | 222 | 222 |  |
D2h | C2v, C2h | |
E, C2,  v, v,  v' v' |
4 | C2v | mm2 | mm2 |  |
 |
D2h | D2, C2h |
E, C2, C2', C2'',
i,  , ,  ', ',  '' ''
|
8 | D2h (Vh) | mmm |
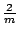 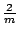 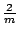 |
 |
 |
D2h | |
|
Rhombic symmetry for defects in crystals is often divided into two
types: Type I: C2 coincides with the [110] direction and C2' and C2'' with [001] and [1-10] directions respectively (or,  v
and v
and  v'
coincide with the planes (1-10) and (001)).
Also belonging to type I are centres for which
C2 coincides with [001] and v'
coincide with the planes (1-10) and (001)).
Also belonging to type I are centres for which
C2 coincides with [001] and
 v
and v
and  v'
with (110) and (1-10). v'
with (110) and (1-10).Type II: C2 axis coincides with [001] and the axes C2' and C2'' with [100] and [010], (or, alternatively,  v
and v
and  v' coincide with (010) and (100)). v' coincide with (010) and (100)).
|
||||||||
| Monoclinic | ||||||||
| E, C2 | 2 | C2 | 2 | 2 |  |
C2h | Cs, Ci | |
E,  h h |
2 | Cs (C1h) | m | m |  |
C2h | C2, Ci | |
E, C2, i,  h h |
4 | C2h | 2/m | 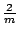 |
 |
 |
C2h | D2, C2v |
| Triclinic | ||||||||
| E | 1 | C1 | 1 | 1 |  |
Ci | ||
| E, i | 2 | Ci (S2) | 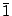 |
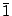 |
 |
Ci | Cs, C2 | |
| Trigonal | ||||||||
| E, C3, C32 | 3 | C3 | 3 | 3 |  |
S6 | ||
| E, C3, C32, i, S65, S6 | 6 | S6 (C3i) | 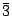 |
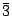 |
 |
 |
S6 | C6, C3h |
| E, 2C3, 3C2 | 6 | D3 | 32 | 32 |  |
D3d | C3v | |
E, 2C3, 3 v v |
6 | C3v | 3m | 3m |  |
 |
D3d | D3 |
E, 2C3, 3C2, i, 2S6, 3 d d |
12 | D3d | 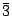 m m |
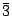 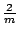 |
 |
 |
D3d | C6v, D6, D3h |
| Hexagonal | ||||||||
| E, C6, C3, C2, C32, C65 | 6 | C6 | 6 | 6 |  |
C6h | S6, C3h | |
E, C3, C32,  h,
S3, S32 h,
S3, S32 |
6 | C3h (S3) | 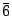 |
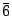 |
 |
 |
C6h | S6, C6 |
E, C6, C3, C2, C32, C65, i, S32, S65,  h,
S6, S3 h,
S6, S3 |
12 | C6h | 6/m | 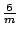 |
 |
 |
C6h | |
| E, 2C6, 2C3, C2, 3C2', 3C2'' | 12 | D6 | 622 | 622 |  |
D6h | C6v, D3d, D3h | |
E, 2C6, 2C3, C2, 3 v,
3 v,
3 d d |
12 | C6v | 6mm | 6mm |  |
 |
D6h | D6, D3d, D3h |
E, 2C3, 3C2,  h,
2S3, 3 h,
2S3, 3 v v |
12 | D3h | 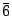 m2 m2 | 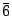 m2 m2 |
 |
 |
D6h | D6, D3d, C6v |
E, 2C6, 2C5,
C2, 3C2', 3C2'',
i, 2S3, 2S6,  h,
3 h,
3 d,
3 d,
3 v v |
24 | D6h | 6/mmm |
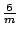 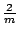 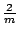
|
 |
 |
D6h | |
| Non-Crystallographic | ||||||||
| Operations | Order | Schönflies Symbol |
International Symbol |
Full Symmetry Symbol |
Correlation Table |
Irred. Rep. products |
x i | Isomorph. with |
E,
2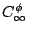 |
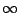 |
C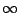 |
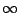 |
- | - | C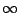 h h |
||
E,
2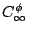 ,
i,
2 ,
i,
2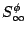 |
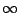 |
C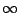 h h |
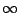 /m /m |
- | - | C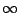 h h |
||
E,
2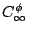 , ,
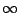  v v |
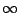 |
C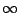 v v |
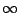 m m |
- | - | D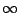 h h |
||
E,
2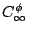 , ,
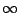  v,
i,
2 v,
i,
2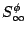 , ,
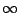 C2 C2 |
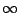 |
D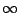 h h |
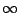 /mm /mm |
- | - | D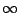 h h |
||
| E, C5, C52, C53, C54 | 5 | C5 | 5 | - |  |
S10 | ||
| E, S8, C4, S83, C2, S85, C43, S87 | 8 | S8 | - | - |  |
 |
C8h | |
| E, 2C5, 2C52, 5C2 | 10 | D5 | - | - |  |
D5d | C5v | |
E, 2C5,
2C52,
5 v v |
10 | C5v | - | - |  |
 |
D5d | D5 |
E,
C5,
C52,
C53,
C54,
 h,
S5,
S57,
S53,
S59 h,
S5,
S57,
S53,
S59
| 10 | C5h | - | - |  |
 |
C10h | |
E, 2S8, 2C4, 2S83, C2, 4C2',
4 d d |
16 | D4d | - | - |  |
 |
D8h | |
E,
2C5,
2C52,
5C2,
i,
2S10,
2S103,
5 d d |
20 | D5d | - | - |  |
 |
D5d | D5h |
E,
2C5,
2C52,
5C2,
 h,
2S5,
2S52,
5 h,
2S5,
2S52,
5 d d |
20 | D5h | - | - |  |
 |
D10h | D5d |
E
2S12
2C6
2S4
2C3
2S125
C2
6C2'
6 d d
| 24 | D6d | - | - |  |
 |
D12h | |
| E, 12C5, 12C52, 20C3, 15C2 | 60 | I | - | - |  |
Ih | ||
E,
12C5,
12C52,
20C3,
15C2,
i,
12S10,
12S103,
20S6,
15
|
120 | Ih | - | - |  |
Ih | ||