
Categorisation of point groups by their unit cells


|
Categorisation of point groups by their unit cells |

|
The various categorisations of classes of point groups can be arranged by the values taken of their unit cell lengths and angles, as shown in this diagram. The order of the group is defined as the number of symmetry operations. Follow the links to the character tables for each point group, or return to the top. Also the main point groups are listed with the common notations and symmetry operations.
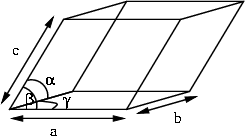
| Conditions | Point Groups | Order | Orthographic projection |
|
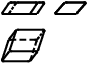
| Triclinic |
a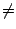 b b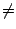 c c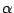 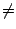 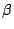 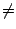 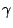
|
C1 | 1 |
|
| Ci | 2 | |||
| Monoclinic |
a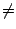 b b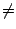 c c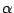 = =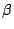 = =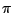 /2 /2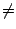 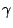
|
Cs (C1h) | 2 |
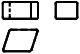
|
| C2 | 2 | |||
| C2h | 4 | |||
| Orthorhombic |
a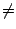 b b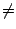 c c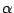 = =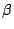 = =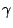 = =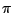 /2 /2
|
C2v | 4 |

|
| D2 | 4 | |||
| D2h | 8 | |||
| Tetragonal |
a=b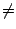 c c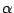 = =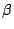 = =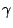 = =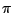 /2 /2
|
C4 | 4 |
|
| S4 | 4 | |||
| C4h | 8 | |||
| D2d | 8 | |||
| C4v | 8 | |||
| D4 | 8 | |||
| D4h | 16 | |||
| Trigonal |
a=b=c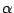 = =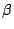 <2 <2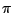 /3, /3,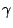 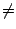 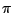 /2 /2
|
C3 | 3 |
 |
| S6 | 6 | |||
| C3v | 6 | |||
| D3 | 6 | |||
| D3d | 12 | |||
| Hexagonal |
a=b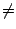 c c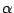 = =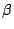 = =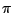 /2, /2,
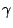 =2 =2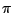 /3 /3
|
C3h | 6 |
|
| C6 | 6 | |||
| C6h | 12 | |||
| D3h | 12 | |||
| C6v | 12 | |||
| D6 | 12 | |||
| D6h | 24 | |||
| Cubic* |
a=b=c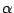 = =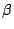 = =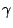 = =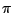 /2 /2
|
T | 12 |
|
| Th | 24 | |||
| Td | 24 | |||
| O | 24 | |||
| Oh | 48 | |||