
Categorisation of point groups by symmetry operations


|
Categorisation of point groups by symmetry operations |

|
This table lists point group symmetries along with their symmetry
operations, the order of the group (i.e. the number of symmetry
operations) and common notations.
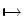 links to a correlation table, and
links to a correlation table, and 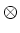 links to tables of products of irreducible representations. The group produced by combination with inversion is listed under "x i". This, in the case of crystolographic point groups, is the Laue class which corresponds to the symmetry of reciprocal space. Isomorphic groups are also listed where
character tables are available.
links to tables of products of irreducible representations. The group produced by combination with inversion is listed under "x i". This, in the case of crystolographic point groups, is the Laue class which corresponds to the symmetry of reciprocal space. Isomorphic groups are also listed where
character tables are available.
| Cubic | ||||||||
| Tetragonal | ||||||||
| Orthorhombic | ||||||||
| Monoclinic | ||||||||
| Triclinic | ||||||||
| Trigonal | ||||||||
| Hexagonal | ||||||||
| Operations | Order | Schönflies Symbol |
International Symbol |
Full Symmetry Symbol |
Correlation Table |
Irred. Rep. products |
x i | Isomorph. with |
| E, C6, C3, C2, C32, C65 | 6 | C6 | 6 | 6 | 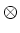 |
C6h | S6, C3h | |
E, C3, C32, 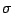 h,
S3, S32 h,
S3, S32 |
6 | C3h (S3) | 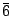 |
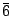 |
 |
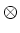 |
C6h | S6, C6 |
E, C6, C3, C2, C32, C65, i, S32, S65, 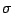 h,
S6, S3 h,
S6, S3 |
12 | C6h | 6/m | 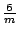 |
 |
 |
C6h | |
| E, 2C6, 2C3, C2, 3C2', 3C2'' | 12 | D6 | 622 | 622 | 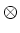 |
D6h | C6v, D3d, D3h | |
E, 2C6, 2C3, C2, 3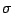 v,
3 v,
3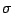 d d |
12 | C6v | 6mm | 6mm | 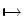 |
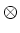 |
D6h | D6, D3d, D3h |
E, 2C3, 3C2, 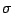 h,
2S3, 3 h,
2S3, 3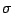 v v |
12 | D3h | 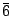 m2 m2 | 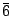 m2 m2 |
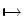 |
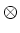 |
D6h | D6, D3d, C6v |
E, 2C6, 2C5,
C2, 3C2', 3C2'',
i, 2S3, 2S6, 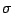 h,
3 h,
3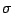 d,
3 d,
3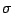 v v |
24 | D6h | 6/mmm |
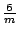 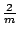 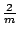
|
 |
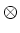 |
D6h | |
| Non-Crystallographic | ||||||||
| All | ||||||||