
Symmetry Operations and Character Tables


|
Symmetry Operations and Character Tables |

|
All the character tables are laid out in the same way, and some pre-knowledge of group theory is assumed. In brief:
| E | The identity transformation (E coming from the German Einheit, meaning unity). |
| Cn |
Rotation (clockwise) through an angle of 2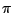 /n radians, where n is an integer.
The axis for which n is
greatest is termed the principle axis. /n radians, where n is an integer.
The axis for which n is
greatest is termed the principle axis.
|
| Cnk |
Rotation (clockwise) through an angle of 2k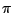 /n radians. Both n and k are
integers. /n radians. Both n and k are
integers.
|
| Sn |
An improper rotation (clockwise) through an angle of 2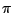 /n radians. Improper rotations are
regular rotations followed by a reflection in the plane
perpendicular to the axis of rotation. Also known as
alternating axis of symmetry and rotation-reflection
axis. /n radians. Improper rotations are
regular rotations followed by a reflection in the plane
perpendicular to the axis of rotation. Also known as
alternating axis of symmetry and rotation-reflection
axis.
|
| i |
The inversion operator (the same as S2). In
Cartesian coordinates, (x, y, z) 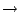 (-x, -y, -z).
Irreducible representations that are even under this symmetry
operation are usually denoted with the subscript g for
gerade (german=even), and those that are odd are denoted
with the subscript u for ungerade (german=odd). (-x, -y, -z).
Irreducible representations that are even under this symmetry
operation are usually denoted with the subscript g for
gerade (german=even), and those that are odd are denoted
with the subscript u for ungerade (german=odd).
|
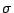
|
A mirror plane (from the German word for mirror - Spiegel). |
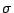 h h
|
Horizontal reflection plane - passing through the origin and perpendicular to the axis with the `highest' symmetry. |
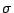 v v
|
Vertical reflection plane - passing through the origin and the axis with the `highest' symmetry. |
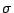 d d
|
Diagonal or dihedral reflection in a plane through
the origin and
the axis with the `highest' symmetry, but also bisecting the
angle between the twofold axes perpendicular to the symmetry
axis. This is actually a special case of 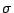 v. v.
|
It often occurs for a point group that there are inequivalent operations of the same type. For example there are three C2 operations in the D2d point group, two of which are inequivalent to the third. In such cases the different operations may be distinguished with a `prime' or by indicating some Cartesian reference (such as the x, y, and z related C2 operations in D2).
There is an important note to bear in mind regarding Cubic point groups. Within this site, this term is used in the crystallographic sense, but there is (unfortunately) an alternative definition of cubic. The expression 'cubic point groups' may refer to all point groups with indistinguishable cartesian axes. This means that for example all three moments of inertia are identical. All cubic point groups can be derived from the Platonic solids.