Recursion

Functions that call themselves

God is subtle but he is not malicious.
Einstein

Recursion is an extremely simple concept: a function simply calls itself.

Recursion refers to a function that calls itself either directly or indirectly.

The "call myself again" test

Of course, a function can't always call itself, that would create an infinite loop, so all recursive functions have some sort of test before they call themselves.

void myfun(some_args) {

 /* Do some stuff */
  if (some_test)
     myfun(some_other_args);
}

A slightly more sophisticated alternative is to have a loop for the function to call itself as many times as possible and for that loop to be empty when the function does not need to call itself.

There must always be a test (or a possibly-empty loop) to see if a function must call itself.

A better test

A nice variation on the above is for the function to always call itself and for the (next generation of ) the function to see if it actually needed to be called and to immediately return if not:

void myfun(some_args) {
  if (I_didnt_need_to_be_called)
    return;

    /* Do some stuff */
    myfun(some_other_args);
}

Where it works this is neater (as we do the test only once and the calling function doesn't need to worry about it).

A function that examines its arguments to see if it doesn't need to do anything is always easier to use than one where the person calling it has to do so.

A function may itself contain the test and immediately return if nothing is required..

Try googling the word "recursion"

The test is the key

Recursion can lead to subtle errors: either something gets treated twice or not at all, or our recursion goes into an infinite loop.

The key to recursion is to understand the "test" inside the recursive function that decides whether or not it calls itself again.

Automatic and static variables

By default variables and arrays inside functions are automatic, that is they automatically come into existence when a function starts and are automatically destroyed when it returns. This also means that if a function calls itself then each instance of the function has its own copies of variables.

When functions call themselves each instance has its own local variables, unless they are static.

Occasionally we may need to have a variable within a function keep its value between calls. The static keyword does this.

Static variables retain their values between calls to functions.

Static variables are permanent and initialised before the start of the program. Unlike ordinary variables, if no explicit initial value is specified a value of zero (or NULL for pointers) is assumed:

 Static variables are intialised once, when the program starts to run and default to zero if not explicitly initialised.

Static variables are initialised to zero by default.

Example of static variables

The following, somewhat strange, function keeps track of the sum of its arguments. As a diagnostic, it also keeps track of how many times it has been called.

// static demonstration
#include <stdio.h>
#include <math.h>

double addup(double k) {
  static int called;
  static double sum;

  sum += k;
  printf("k is %g new sum is %f\n", k, sum);
  printf("The function has been called %d times\n", ++called);
  
  return sum;
}


int main() {
  int i, max=5;
  double mysum;
  
  for(i = 1; i <= max; ++i)
    mysum = addup(sqrt(i));
  
  printf("The sum of the square roots of 1 to %d is %g\n", 
   max, mysum);
  return 0;
}

Step through this code


	    

1. Step through the above "Key example".
2. To illustrate static variable.
1. Step through the above "Key example".
2. Notice how the two variables called and sum exist even before the program starts and are initialised to zero.
3. Step through the code. When the addup() function is called notice how it accesses its own "normal" (automatic) variables and its static variables.
4. Notice how the changes to called and sum are permanent.

A simple example of recursion

Example: a factorial function

The simplest example of recursion is the following somewhat pretentious factorial function:

long factorial(int i) {
  if ( i > 0 )
    return  i * factorial(i - 1);
  
  return 1;
}

Step through this code

NB: in the above stepped example, the initial call to factorial() from main() is labelled just "factorial", recursive calls are labelled "factorial-2", "factorial-3", etc.

This illustrates the concepts of recursion:

1. A function called factorial() that calls itself.
2. A test to make sure the sequence of function calls stops at some point
3. A local variable, in this case called "i", which local to each invocation of factorial(): when factorial() calls itself each instance has its own copy of i.

It also illustrates one possible pitfall: it's possible to use recursion just to show off. The above example would have been better written as a simple loop.

Error checking and wrappers

It's always nice if a function does some sanity checking on its arguments and we could add some simple argument error checking as follows:

long factorial(int i) {
  if ( i > 0 )
    return  i * factorial(i - 1);
  else if (i < 0 ) {
    fprintf(stderr, "Factorial must be positive\n");
    return -1;
  }

  return 1;
}

Another option would be to make the publicly-callable function a wrapper around the real function. This avoids the test being done many times over when it only needs to be done once:

// The actual factorial function
long factorial_real(int i) {
  if ( i <= 1 )
    return 1;
  return  i * factorial_real(i - 1);
}

// Publically-callable front-end to the 
// factorial function with error checking
long factorial(int i) {
  if (i < 0 ) { // Error check
    fprintf(stderr, "Factorial must be positive\n");
    return -1;
  }
 return factorial_real(i);
}

Step through this code

This is slightly over the top in this case but is a useful illustration.

When recursion goes wrong

Recursion can be hard to debug. In non-recursive programs we can get a long way by knowing what function we are in and what function called it and with what arguments. But with problems with recursion we know what the function is and it's usually called by itself! The biggest problem tends to be the internal test: either the recursion never stops or some possibilities get missed out.

The biggest source of problems with recursion is the internal test.

Imagine we had made a mistake in our previous rather over-the-top way of calculating a factorial:

long factorial(int i) {

  if ( 1 > 0 ) // Bug!
    return  i * factorial(i - 1);
  return 1;
}

You can see what it's meant to do but we've written '1' instead of 'i' so it will go on for ever. The first stage of debugging is just to print out its arguments:

long factorial(int i) {

  fprintf(stderr, "i: %d\n", i);
  if ( 1 > 0 ) // Bug!
    return  i * factorial(i - 1);
  return 1;
}

}

Try printing out the function's arguments.

Keeping track of the depth

We can get even more details by adding extra debugging argument to tell us the depth. The most obvious way to do this (we shall see another below) is just to add an extra parameter to the function for the function to increment this every time it calls itself:

#include <stdlib.h>
#include <assert.h>

long factorial(int i, int depth) {
  int d;

  // Print depth information for debugging
  for(d = 0; d <= depth; ++d)
    fprintf(stderr, "  ");
  fprintf(stderr, "i: %d (depth %d)\n", i, depth);

  // If we have gone too deep abort the program
  assert( depth < 12);

  if ( 1 > 0 ) // Bug!
    return  i * factorial(i - 1, depth + 1);
  return 1;
}

When debugging recursion the depth is always a useful number to know!

We should be prepared to add some "depth" debugging to our recursive routine.

Here we have done several things:

• We have added an extra 'depth' argument which we increment by one every time.
• We have indented the output according to the depth. This isn't necessary but it is nice.
• Finally, and rather extremely, if factorial() goes too deep we kill the program using assert(). This is only useful when we are running under the debugger as we can look at the "layers" of recursive call.

assert(expression) is defined inside assert.h and kills the program if expression is false.

The output looks like this:

 
  i: 3 (depth 0)
    i: 2 (depth 1)
      i: 1 (depth 2)
        i: 0 (depth 3)
          i: -1 (depth 4)
            i: -2 (depth 5)
              i: -3 (depth 6)
                i: -4 (depth 7)
                  i: -5 (depth 8)
                    i: -6 (depth 9)
                      i: -7 (depth 10)
                        i: -8 (depth 11)
                          i: -9 (depth 12)
                            i: -10 (depth 13)
recurse-err3.c:13: factorial: Assertion `depth < 12' failed.
Abort (core dumped)

Using a wrapper

It may be very inconvenient to add an extra argument to our routine because it is called elsewhere. One way around this is to rename our "real" function, say to factorial_debug(), and create a simple wrapper:

long factorial_debug(int i, int depth) {
  // Real factorial code here...
}

long factorial(int i) {
  return  factorial_debug(i, 0);
}

Using a static depth variable

The debugging codes above have the disadvantage of having to add an extra parameter to our function. An alternative way of keeping track of the depth is by having an in-function static variable.

We can use a static variable to keep track of the depth as follows:

1. Each time the function starts we increment the value of depth by one.
2. Immediately before the function returns we decrement the value of depth by one.

If a recursive function has more than one place it returns we must take care to decrement the value of depth at each place. This is a particular issue in our case where one of the return statements reads:

    return  i * factorial(i - 1);

In order to decrement depth after the recursive call we have to declare a temporary variable:

  long fact1;
    fact1 =  i * factorial(i - 1);
    --depth;
    return fact1;

The complete code is shown below with the new parts highlighted in bold red. It can be seen that the code avoids having to declare an extra debugging paramater at the expense of some extra code inside the function.

#include <stdlib.h>
#include <assert.h>

long factorial(int i) {
  long fact1;
    static int depth;
  ++depth;
  
  // Print depth information for debugging
  //  for(int d = 0; d <= depth; ++d)
  //   fprintf(stderr, "  ");
  // fprintf(stderr, "i: %d (depth %d)\n", i, depth);

  // If we have gone too deep abort the program
  assert( depth < 12);

  if ( i > 1 ) {
    fact1 =  i * factorial(i - 1);
    --depth;
    return fact1;
  }
  
  --depth;
  return 1;
}

Step through this code

 
			

Each method has its own advantages and disadvantages and as always we should choose the simplest and clearest option in any given situation.

The order of the actions

Often a recursive function has the choice of "do an action then call itself recursively" or "call itself recursively then do an action":

void myfun(some_args) {
  if (I_didnt_need_to_be_called)
    return;

  // Do some stuff here...
  myfun(some_other_args);
}

void myfun(some_args) {
  if (I_didnt_need_to_be_called)
    return;

  myfun(some_other_args);
  // Do some stuff here...
}

When a function performs an action and calls itself recursively it's usually important to do them in the right order.

Directionality and trees

Our factorial is an example of a process with a clear order: The argument decreases by one each time. In this sense every recursive call has a "parent" and there is no danger of any loops.

Trees

Sometimes a collection of data structures may also have an inbuilt hierarchy "direction". Consider the example of folders (or directories) on a computer. Folders may contain sub-folders and/or normal files but any given folder may only be inside one other flder and there are no loops (a folder may not be its own decendent). We may imagine a recursive "list the contents of this folder and all its decendents" function as:

This isn't always the case however: things may have multiple parents (as in the example of real-life family trees), or the concept of parenthood may not even exist, and/or we may have loops.

When data can contain loops we must make sure our recursive functions do not also loop, usually by "marking" visited nodes in some way.

The order in which this is done inside the function is critical and must be:

1. Check to see if node has been visited (or there is another reason to do nothing), and if so return.
2. Mark the node as visted.
3. Do stuff and Recurse.

The correct order: Check, Mark, Recurse

void myfun(some_args) {
  if (node_has_been_visited || I_didnt_need_to_be_called)
    return;                      //Check 

  // Mark this node as visited;  //Mark 

  // Do some stuff here...
  myfun(some_other_args);        //Recurse
}

We show some incorrect examples in the common mistakes with recursion page.

Flood fill

This example doesn't use structures at all, it's simply an array of characters (NB: in real life we would probably use integers, we are using characters here for clarity.)

A common situation, with a number of variations, is when we have a rectangular grid of values, typically representing an image, and we wish to identify "islands", i.e. sets of neighbouring pixels (or cells) with the same value.

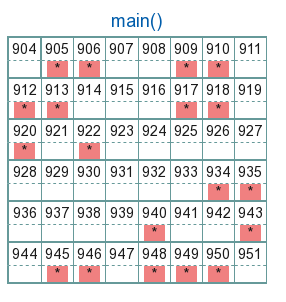
The flood fill function

As an example of flood fill let's imaging we have an NY by NX character array where spaces represent nothing being there and a star, '*', represents something there. We wish to find and label the islands. In this case we assume diagonal cells are connected.

This way of storing the data totally non-recursive: just a two-dimensional array of chars. But the relationship is recursive: cells are connected to their neighbours, which are connected to their neighbours, which are connected to their neighbours, which are connected to their neighbours...

The following function looks for islands of stars ('*') in a sea of spaces or other characters and replaces then with the character area_id (typically 'A', 'B', 'C' etc). As a bonus it returns the size of the island.

// See if point (x,y) is occupied and if so mark it as "aread_id"
// and flood-fill its neighbours.
int floodfill(char image[NY][NX], int x, int y, char area_id) {

  // 1. Check if we need to do anything
  if ( x < 0 || x >= NX || y < 0 || y >= NY || image[y][x] != '*' ) {
    return 0;
  }

  // 2. Mark as already counted  BEFORE the recursive calls
  image[y][x] = area_id;

  // 3. Start at 12-o'clock and go round the cell clockwise
  // trying each of its neighbours in the following order:
  //
  // 8|1|2
  // 7| |3
  // 6|5|4
  //
  return 1 + floodfill(image, x, y-1, area_id)  // Call 1: 12 o'clock
    + floodfill(image, x+1, y-1, area_id)      // Call 2: 1  o'clock
    + floodfill(image, x+1, y, area_id)        // Call 3: 3  o'clock
    + floodfill(image, x+1, y+1, area_id)      // Call 4: 4  o'clock
    + floodfill(image, x, y+1, area_id)        // Call 5: 6  o'clock
    + floodfill(image, x-1, y+1, area_id)      // Call 6: 7  o'clock
    + floodfill(image, x-1, y, area_id)        // Call 7: 9  o'clock
    + floodfill(image, x-1, y-1, area_id) ;    // Call 8: 11 o'clock
}

Notes

1. Before we do anything we see if the function needs to do anything, if not we immediately return.
   • We check the co-ordinates are in range before checking the pixel (image) value at that point.
2. Then the first thing we do is to mark the pixel as filled.
3. Then we try each of its neighbours, in this case starting with the pixel immediately above ("twelve o'clock") and working round clockwise.

Had we reversed the last two steps then the function would have been forever calling itself.

Showing the depth

Recall that the depth is always a useful number to know. We can add a little depth depth debugging by initially changing the grid character to '0', '1', '2', according to the depth, then doing the recursive function calls and only setting it to the proper character at the end:

The integer value of '1' is the integer value of '0' plus one, and so on up to the integer value of '9' being the integer value of '8' plus one.

int floodfill(int x, int y, char image[NY][NX], char area_id, int depth) {
  int count;
  if ( x < 0 || x >= NX || y < 0 || y >= NY || image[y][x] != '*' ) {
    return 0;
  }


  // When finished debugging do NOT remove this line, change it to area_id
  
  image[y][x] = '0' + (depth % 10);  // Was area_id

  count  = 1 + floodfill(x, y-1, image, area_id, depth + 1)
     + floodfill(x+1, y-1, image, area_id, depth + 1)
     + floodfill(x+1, y, image, area_id, depth + 1)
     + floodfill(x+1, y+1, image, area_id, depth + 1)
     + floodfill(x, y+1, image, area_id, depth + 1)
     + floodfill(x-1, y+1, image, area_id, depth + 1)
     + floodfill(x-1, y, image, area_id, depth + 1)
     + floodfill(x-1, y-1, image, area_id, depth + 1) ;
  
  
  image[y][x] = area_id;
  return count;
}

The whole program

All we need to do now is to go over each point in the image and call floodfill() for each point that needs it and update the area_id character if an island is found.

Notes:

1. To save time we are skipping over must of the steps of the program and only pausing on accesses to the image components and top-level calls to floodfill()
2. We are not showing the values of the variables inside main() except for the image grid which we are showing without its name and with non-blank elements colour-coded for clarity. Thus the image looks like this:
   

#include <stdio.h>
// Demonstrate a flood fill, using it to count and label non-empty
// contiguous regions in an image.  

#define NX 8
#define NY 6
void setup(int nx, int ny, char image[NY][NX]);

int floodfill(int x, int y, char image[NY][NX], char area_id, int depth) {
  int count;
  if ( x < 0 || x >= NX || y < 0 || y >= NY || image[y][x] != '*' ) {
    return 0;
  }


  // When finished debugging do NOT remove this line, change it to area_id
  
  image[y][x] = '0' + (depth % 10);  // Was area_id

  count  = 1 + floodfill(x, y-1, image, area_id, depth + 1)
     + floodfill(x+1, y-1, image, area_id, depth + 1)
     + floodfill(x+1, y, image, area_id, depth + 1)
     + floodfill(x+1, y+1, image, area_id, depth + 1)
     + floodfill(x, y+1, image, area_id, depth + 1)
     + floodfill(x-1, y+1, image, area_id, depth + 1)
     + floodfill(x-1, y, image, area_id, depth + 1)
     + floodfill(x-1, y-1, image, area_id, depth + 1) ;
  
  
  image[y][x] = area_id;
  return count;
}

#define IMAX 26
int main() {
  char image[NY][NX];
  int found = 0;
  int ix, iy, nf;
  char letters[32] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
  int sizes[IMAX];
  
  
  setup(NX, NY, image);
  
  for(iy = 0; iy < NY; ++iy)
    for(ix = 0; ix < NX; ++ix) {
      nf = floodfill(ix, iy, image, letters[found], 0);
      if ( nf ) {
  sizes[found] = nf;
  ++found;
      }
    }
  
  printf("I found %d islands\n", found);
  for (ix = 0; ix < found; ++ix)
    printf("Island %c size %d\n", letters[ix], sizes[ix]);
  return 0;
}

Step through this code

This will fill the first island/region with the value 'A', the second with the value 'B', etc. and print the total number of islands found together with their sizes.

If "mark as done" in the wrong place

In the following example we have disregarded our comment and are doing the "mark as done" after the recursive calls. We have put in a depth check to stop the program from entering an infinite recursive loop.

Recursive data structures

NB: this is a fairly advanced topic.

One of the reasons why recursion is so useful is that we often have to deal with recursive things.

Example: a passive electrical circuit

A simple electrical circuit consists of resistors, capacitors and inductors in series or in parallel. But a more complicated cicuit may consist of sub-circuits in parallel. How do we find the impedance of (a resistor in series with a capacitor) in parallel with (another resistor in series with an inductor) ?

It turns out it's actually very easy. First, consider a simple data structure to represent a single passive electrical component. It has to tell us two things: the type of the component and its value.

Using named constants for the component type

Rather than using strings to represent the component type it's easier to use integer values, such as 0, 1. But we wish to avoid code like:

int type; // 0 is resistor, 1 capacitor, 2 inductor

as it becomes extremely easy to make a mistake. One solution is to use #define:

#define Resistor  0
#define Capacitor 1
#define Inductor  2

We can then use the words "Resistor" etc throughout the code rather than "0".

Enumerations

We cover enumerations more thoroughly in the next lecture.

C provides a more sophisticated way of doing this using enumerations. The following code:

typedef enum { Resistor, Capacitor, Inductor } Type;

The structure definition

We can now define a structure for a component as:

typedef enum { Resistor, Capacitor, Inductor } Type;
typedef struct component {
  double value;
  Type type;
} Component;

The impedance function

We can easily write a simple function to calculate the impedance of a single component at a specific frequency, taking a little care about division by zero for very low frequencies when dealing with capacitors.

Naive capacitor impedance

For a capacitor we might first write the code to return the impedance as:

 return 1.0/(2 * PI * I * c->value * freq);

But this has problems when the frequency is zero. We can get round this with the following code using a suitable value for INFINITY :

    // Handle DC and v low frequencies
    denom = 2 * PI * c->value * freq;
    if ( denom < 1.0/INFINITY )
     denom = 1.0/INFINITY;
    return 1.0/(I * denom);

The code

#include <complex.h>
#define INFINITY 1e100
#define PI 3.14159265358979

double complex impedance(Component *c, double freq) {
  double denom;
  
  switch (c->type) {
  case Resistor:
    return c->value;

  case Inductor:
    return 2 * PI * I * c->value * freq;

  case Capacitor:
    // Handle DC and v low frequencies
    denom = 2 * PI * c->value * freq;
    if ( denom < 1.0/INFINITY )
     denom = 1.0/INFINITY;
    return 1.0/(I * denom);
  }
}

The question is "how do we combine these to handle more-complicated circuits?".

Series and parallel circuits

Given an array of pointers to components arranged in series, the total impedance is just the sum of the individual impedances:

  // Series impedance
  double complex zs = 0;
  for (int i = 0; i < n; ++i)
    zs += impedance(component[i], freq);

The parallel case is almost as simple, it's the reciprocal of the sum of the reciprocals:

  // Parallel impedance
  double complex zp = 0;
  for (int i = 0; i < n; ++i)
    zp += 1.0/impedance(component[i], freq);
  
  zp = 1.0/zp;

This gives us the germ of an idea: given that we can find the impedance of a list of components arranged in series we can think of a series of components as a single, multipart component. The same applies to components arranged in parallel. So we can combine these multi=part components to build more-complicated circuits.

Representing series and parallel circuits

In this situation our instinctive reaction may be to have two types of structures, one for individual components and one for circuits consisting of several components. But we can make life much simpler for ourselves by one simple, but perhaps slightly counterintuitive, trick: recognising that a "circuit" may consist of just one component. Thus we abolish the distinction between a component and a circuit. We say that a single component is just a circuit with only one thing in it and just merge the two structures together to look like this:

typedef enum  type { Resistor, Capacitor, Inductor, Series, Parallel } Type;

typedef struct component {
  double value;
  Type type;
  unsigned int n;             // If parallel or serial
  struct component *nodes[];  // If parallel or serial
} Component;

Flexible arrays

The definition above apparently has a huge flaw: it doesn't say the size of the final array! In fact this is a handy feature, avalable only for arrays that are the final member of a dynamically-allocated array.

Imagine first that the array had an actual size, say 2. Then the following code would allocate an array with an array of two pointers:

 Component *c;
 c = malloc( sizeof *c);	    

But the only thing a compiler cares about is where an array starts, not where it ends (that's up to us). So a neat trick is to write:

 Component *c;
 c = malloc( sizeof *c + n * sizeof *c->nodes);	    

This would allocate us enough space for a structure with an array of n+2 pointers. So C allows us to do away with the dummy array size altogether and to declare an array of size zero and to then allocate as much memory as we like for the array to expand into. Of course, this can only work if the array is the final member of the structure and the memory is dynamically allocated. In this case sizeof *c is the size of the structure with a zero-length final array.

This is an example of what we might called the "Generalised Thing", or possible a "Compound Thing".

The "Generalised Thing"

Given a set of simple "Things" (in our case, electrical components) which can be combined together a useful concept is what we might call a "Generalised Thing". A Generalised Thing is either:

1. A single simple Thing.

   Or:

2. A collection of other Generalised Things, sometimes called nodes or children, plus enough information to know how they are combined together.

This simple, and indeed rather strange concept, is remarkably useful. Notice that it is recursive, each of the nodes may have other nodes, etc.

In our case the simple things are resistors, capacitors and inductors, and there are two ways of combining components, series or parallel. So a "generalised component" or circuit conists of either:

• A resistor or
• A capacitor or
• An inductor or
• Two or more sub-circuits arranged in series or
• Two or more sub-circuits arranged in parallel

Example: foods

If you've ever looked at the ingredients of a supermarket sandwich you may well know what we mean!

This is usually referred to as the list of ingredients. In programming the word "list" is often used for a "generalised thing" that is a simple thing or a collection of other things, a generalised thing that consists of a simple thing and possibly a collection of other things is called a tree. We don't get hung up on the difference, we just make sure we can handle either situation.

Another example of a "Generalised Thing" is a mathematical expression: a mathematical expression may contain a sub-expression in parentheses in which case the sub-expression is treated a a whole new top-level expression and may itself contain parentheses:

x * ( 1 + y * ( z - 2 * (a + b ) ) ) + a * ( x + y )

Example circuit

Consider the following circuit:

Ladder filter, image courtesy of Wikipedia (Fcorthay)

What impedance does this present at Uin if Uout is left open-circuit? Starting from the left, the circuit consists of:

R in series with ( C1 in parallel with ( L2 in series with ( C3 in parallel with ( L4 in series with R))))

The data structure

• How many nodes there are.
• Whether the nodes are in series or parallel
• An array of pointers, one for each node

The recursive impedance function

Our recursive impedance function is now just:

#define NODE_MAX 20

typedef enum  type { Resistor, Capacitor, Inductor, Series, Parallel } Type;

typedef struct component {
  double value;
  Type type;
  unsigned int n;             // If parallel or serial
  struct component *nodes[];  // If parallel or serial
} Component;


#define INFINITY 1e100
#define PI 3.14159265358979
double complex impedance(Component *c, double freq) {
  double complex z = 0;
  double denom;

  switch (c->type) {
  case Resistor:
    return c->value;

  case Inductor:
    return 2 * PI * I * c->value * freq;

  case Capacitor:
    // Handle DC and v low frequencies
    denom = 2 * PI * c->value * freq;
    if ( denom < 1.0/INFINITY )
     denom = 1.0/INFINITY;
    return 1.0/(I * denom);

  case Series:
    for (int n = 0; n < c->n; ++n)
      z += impedance(c->nodes[n], freq);
    return z;

  case Parallel:
    for (int n = 0; n < c->n; ++n)
      z += 1.0/impedance(c->nodes[n], freq);
    return 1.0/z;
  }
}

And we can now handle quite complicated circuits. (For an example of a cicuit this can't handle directly consider a pyramid with the corners as nodes and the vertices being the "wires" each with a component, as in this PDF courtesy of Charles Williams.)

See also the complete circuit program.