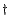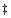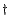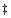|
Irreducible representation products
|

|
Here are listed some helpful general rules for the product of two
irreducible representations. For specific combinations not listed
here, one can work out the product by multiplying the characters of
each irreducible representation and solving the linear combination of
the irreducible representations from the point group that generates
that product. Often ths process is simple, especially when one or
both of the irreducible representations are non-degenerate (in most
cases A or B).
| Non-degenerate |
| A x A |
= |
A |
A x E1 |
= |
E1 |
| B x B |
= |
A |
A x E2 |
= |
E2 |
| A x B |
= |
B |
B x E1 |
= |
E2 |
| A x E |
= |
E |
B x E2 |
= |
E1 |
| B x E |
= |
E |
| A x T |
= |
T |
| B x T |
= |
T |
| Gerade/Ungerade |
Prime/double-prime |
Subscripts on
A or B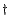 |
| g x g |
= |
g |
' x ' |
= |
' |
1 x 1 |
= |
1 |
| u x u |
= |
g |
'' x '' |
= |
' |
2 x 2 |
= |
1 |
| u x g |
= |
u |
' x '' |
= |
'' |
1 x 2 |
= |
2 |
2-fold
Degenerate |
3-fold Degenerate* |
| E1 x E1 |
= |
A1 + A2 + E2 |
E x T1 |
= |
T1 + T2 |
| E2 x E2 |
= |
A1 + A2 + E1 |
E x T2 |
= |
T1 + T2 |
| E1 x E2 |
= |
B1 + B2 + E1 |
T1 x T1 |
= |
A1 + E + T1 + T2 |
| E x E |
= |
A1 + A2 + E |
T2 x T2 |
= |
A1 + E + T1 + T2 |
| |
|
|
T1 x T2 |
= |
A2 + E + T1 + T2 |
| Caveats |
 |
Groups where there are subscripts 1, 2 and 3 (eg
D2 and D2h)
- here 1x2=3, 2x3=1 and 1x3=2. |
 |
For point groups where the principle axis is C2
or C4
(eg C4 and
D2d), E x E =
A1 + A2 + B1
+ B2.
|
| * |
Td and Oh
|