| Physics and Astronomy |
|
| Physics Home | Study here | Our Teaching | Our Research | Our Centres | News | Work here | EMPS |
Back to top
Introduction to SensorsContents
IntroductionThis is an introduction to some of the physical principles that underly sensors in instrument systems. It is not intended to be definitive, or very detailed, but to give the reader an idea of what is readily achievable with the various systems. I'd welcome corrections and suggestions for improvements. This HTML document supported module PHY3128. ResistanceElectrical resistance is the easiest electrical property to measure precisely over a wide range at moderate cost. A simple digital multimeter costing a few tens of dollars can measure resistances in the range 10 ohm to 10 megohm with a precision of about 1% using a two-wire technique (circuit 1).
The precision of the two-wire method is limited by uncertainties in the values of the lead resistances RL1 and RL2.
Providing the leads are well-matched, three-wire techniques can be used. Circuit 2 employs two matched current sources, I1 and I2, to eliminate the effects of lead resistance providing RL1 = RL2. Circuit 3 is an AC-bridge that is in-balance when RX = RY providing RL1 = RL3. If a lock-in amplifier is used as a null-detector, determination of RX with an extremely low excitation current is possible.
The 4-Wire 'Kelvin' method (circuit 4) is used in difficult cases when lead resistances vary, RX is very small, or when very high accuracy is required. The method is immune to the influence of lead resistance and is limited by the quality of the constant current source and voltage measurement. Thermoelectric voltages can be eliminated by averaging two measurements with the polarity of the excitation current reversed. See also:
Resistive Temperature DetectorsResistance Temperature Detectors (RTD) exploit the fact that the electrical resistivity of metals and alloys varies in a reproducible way with temperature. Platinum, with a temperature coefficient of about 0.0039 K−1, is the most popular material used in this application. An RTD consists of a coil of wire, or a thin-film, with four-wire electrical connections supported in a way that is a compromise between robustness and thermal time-constant. RTDs have excellent accuracy (e.g. 0.025 K at room temperature) over a wide temperature range. At cryogenic temperatures the resistance of metals becomes constant, and it is usual to use a sample of doped-semiconductor as the sensing element. When using RTDs, it is always important to check that the measured resistance is independent of excitation current in order to avoid errors caused by self-heating. See also:
Strain GaugesAt constant temperature, the resistance R of a metal or semiconductor element of area A, length l, resistivity ρ, is $$ R = l \rho / A $$ and when the element is strained this changes by an amount $$ \begin{align*} \Delta R &= { \left ( \frac{\partial R}{\partial l } \right ) \Delta l + \left ( \frac{ \partial R }{ \partial \rho } \right ) \Delta \rho + \left ( \frac{ \partial R }{ \partial A } \right ) \Delta A } \\ &= \frac \rho A \Delta l + { l \over A } \Delta \rho - \frac { \rho l } { A^2 } \Delta A \\ \therefore \frac{ \Delta R }{ R } &= \frac{ \Delta l }{ l } + \frac{ \Delta \rho }{ \rho } - \frac{ \Delta A }{ A }. \end{align*} $$ A typical strain gauge consists of a metal foil, photo-etched to form a serpentine pattern, and mounted on a resin backing film. This is then attached to the structure to be monitored with adhesive. Metal sensor-elements are dominated by the geometric terms in the above equation and therefore they are relatively temperature independent and have a modest gauge factor (i.e. responsivity) of about 2. Semiconductor elements can exploit a large piezo-resistive effect yielding gauge factors of ca 150. However, this is at the expense of temperature stability and some sort of compensation scheme is usually required in practice. Strain gauges are widely used in many applications; they are small, cheap, sensitive and reliable, and many variables (e.g. pressure) can be be used to cause strain. See also: CapacitanceCapacitance can also be measured over a wide range at moderate cost. A simple hand-held meter, and some digital multimeters use a two-wire technique to measure capacitances in the range 100 pF to 1 F with an accuracy of about 1%. Such meters often work by incorporating the unknown capacitor into a relaxation oscillator such as the ramp generator experiment in PHY2003. This charges the unknown capacitance with a known constant current, and the capacitance is calculated from the charging time required for it to reach the threshold voltage. Stray capacitance, typically in the range 10 pF to 10 nF, is the major source of error in capacitance measurements, and must be dealt with using 'guarding' techniques. A high-impedance terminal is guarded by ensuring that it is surrounded by conductors held at the same potential by some means. Circuit&bsp;5 shows how the influence of the stray capacitance to ground associated with a piece of coaxial cable can be eliminated by reconnecting its shield to a low impedance node.
With care (and about 10,000 dollars worth of equipment) it is possible to measure absolute capacitance values to 1 part in 108 using so-called 'AC coaxial bridges'. Capacitive sensors are the most precise of all electrical sensors. A capacitive sensor can be designed to be:
Simple but very precise sensors can be based on the change in geometry of a pair of capacitor plates, or on the effects of introducing conducting material into the capacitor gap. Capacitive Pressure SensorsCapacitive pressure sensors use a thin diaphragm, usually metal or metal-coated quartz, as one plate of a capacitor. The diaphragm is exposed to the process pressure on one side and to a reference pressure on the other. Changes in pressure cause it to deflect and change the capacitance. The change may or may not be linear with pressure and is typically a few percent of the total capacitance. The capacitance can be monitored by using it to control the frequency of an oscillator or to vary the coupling of an AC signal. It is good practice to keep the signal-conditioning electronics close to the sensor in order to mitigate the adverse effects of stray capacitance. Circuit 6 is a schematic example.
Devlopments in silicon-based micro-machine technology have lead to several significant improvements in the performance and usability of capacitve pressure sensors. See also:
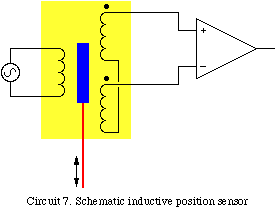
InductanceInductors are probably the least-ideal of discrete components and circuit designers try to avoid using them. As a result, inexpensive handheld inductance meters are available, but not are particularly common (or useful). Their resolution is a few microhenries, limited by the connection leads. Only rather sophisticated impedance analysers can be expected to characterise inductors automatically. Inductive Displacement SensorThe voltage at the output of circuit 7 depends on the position of the high-permeability core (in blue) which is changed with a mechanical linkage (in red). The output signal must be monitored with a phase-senstive detector. There is a null position at the midway point between the two detection coils, which are connected in series-opposition. Commercial devices can have linear ranges from less than 1 mm to more than 250 mm with resolutions of 1 part in 100,000 within the linear range. Inductive displacement transducers can be purchased with integral electronics that internally generates the alternating current and converts the measured signal into a calibrated DC output.
See also:
Thermoelectric EffectsThermoelectric voltages are the most common source of error in low-level voltage measurements. They arise when circuit connections are made using dissimilar metals at different temperatures. In this context, two thermoelectric effects are important. Firstly, the Seebeck effect is the flow of current which arises when the junctions of a circuit made of two different metals are at different temperatures. Secondly, the Thomson effect describes the production of an electromotive force between two points at different temperatures in the same material. Each metal-to-metal junction generates an EMF proportional to its temperature and precautions must be taken to minimise thermocouple voltages and temperature variations in low-level voltage measurements. The best connections are formed using copper-to-copper crimped connections. The table lists thermoelectric voltages for junctions between copper and other metals commonly found in electronics.
Temperature MeasurementThermocouples are reproducible, small and cheap. It is not surprising therefore that they are commonly used to measure temperatures (circuit 8).
If the reference junction J2 is held at a known temperature, the temperature of J1 can be deduced from the measured voltage difference by using standard tables. Maintaining a constant reference temperature is often inconvenient but specialised integrated circuits (e.g. the AD594/5) known as 'electronic cold-junctions' are available. They create and monitor the reference junction within their own packaging, include a precision DC amplifier and linearisation circuitry. See also:
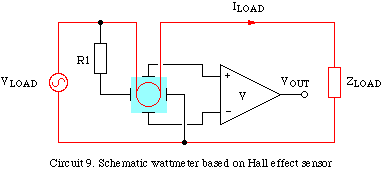
Hall EffectThe phenomenon is known as the Hall effect occurs when a current-carrying conductor is placed in a magnetic field and an EMF (the 'Hall voltage') is generated in the direction mutually perpendicular to both the field and the current flow. Depending on the application, the Hall voltage can be detected with an instrumentation amplifer (DC excitation current) or a lock-in amplifier (AC excitation current). A large range of Hall effect sensors is available commercially, and facilitate the measurement of magnetic fields at frequencies from DC to about 100 kHz, and resolutions of about 10 μT. The high bandwidth and sensitivity of Hall effect sensors can be exploited in many applications. Electric Power MeterThe Hall voltage is proportional to the product of the excitation current and magnetic field. Circuit 9 exploits this property to monitor the power delivered to a load. The Hall device is shown in light blue, a coil (in red) generates a magnetic field that is proportional to the load current, the sensor excitation current passes through R1 and is proportional to the load voltage. The output voltage is therefore proportional to the instaneous power dissipated by the load.
See also:
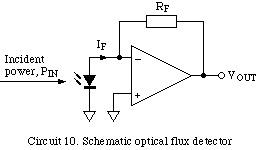
Photoelectric EffectWhen light is absorbed by a semiconductor each photon can, in principle, create an electron-hole pair which can be detected electrically. Photodiodes devices that exploit this possbility. They are pn-junction diodes that have been optimised for use as light detectors. Optical FluxmeterPhotons absorbed by the junction create electron-hole pairs which cause a current proportional to the flux to flow. This current is then amplified. Circuit 10 shows how a transimpedance amplifier can used to amplify the photo-current. The output voltage is proportional to the incident optical flux.
Optimising this type of circuit properly is a tedious job which will be discussed in more detail in the lectures. See also:
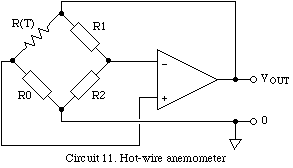
DC-Substitution BridgeThe temperature of a thermometer will fall, other things being equal, if its net rate of energy loss decreases. However, if its temperature is kept constant using heater, it is possible to infer changes in its net power loss/gain from changes in the power that has to be supplied with the heater. This principle can be used to measure any type of energy flux that is absorbed - to known extent - by the thermometer. Hot-Wire AnemometerThe hot-wire anemometer (circuit 11) increases VOUT until the power dissipated in the wire sensing element, and hence its temperature and resistance, has risen to the point where the bridge at equilibrium. Air movement past the wire would cool it, but VOUT increases compensate for the increased dissipation restoring the wire to its equilibrium temperature. The equilibrium behaviour of the system is independent of the heat capacity of the wire. However, the dynamic response, and noise figure, are both improved by minimising the size of the wire.
See also:
|