The first is due to Born and Oppenheimer who argue that, since the nuclear masses are so much larger than those of the electrons, then we can treat the nuclear motion classically and reduce the Schrödinger equation to one only involving the electrons moving in a potential of fixed nuclear sites denoted by R. The solution of this equation is the structural potential energy E(R). To determine dynamical quantities like vibrational frequencies and diffusion barriers, we need then to solve the classical problem of the nuclei moving in the force field .

Let us now consider the Schrödinger equation of the electrons in a field of frozen nuclei. This equation still cannot be solved exactly because of the inter-electronic Coulomb terms, . If these terms were neglected, then the Schrödinger equation is separable and the exact wavefunction can be written down as a sum of product orbitals where are the eigenfunctions of the one-electron Hamiltonian. Of course, we must require that the total wavefunction is antisymmetric and this can be achieved by a suitable sum over the product orbitals. For, example for the H molecule, the antisymmetric wavefunction is

This type of wavefunction is called a Slater determinant and is specified by the electronic configuration, ie. a listing of the orbitals occupied by the N electrons.

The neglect of the electron-electron interaction term is too extreme to make this theory useful and various attempts have been made to take this interaction into account. There are two principal schemes: Hartree-Fock (HF) and density functional theory (DFT). Both of these replace the electrostatic potential acting on electron i by the other electrons, ie.  by an average over the positions of the other electrons. Thus this potential becomes . Clearly the Schrödinger equation is then separable and we can write the wavefunction as a Slater determinant. In these theories, the effective potential is composed of two terms: the Hartree potential and the exchange-correlation potential . The former is the electrostatic potential due to the electron density of charge n(r) at point r. The density is determined by the probability of finding a electron at the point, or

Here, the sum is over the occupied orbitals. The exchange-correlation potential differs in the two theories. In HF, it is a complicated function determined by all the orbitals . In DFT, it is rigorously determined only by the electron density. This is an important result but the precise dependence on density is not known except for a particular problem: the homogeneous electron gas. In this case, the equations have been solved numerically and the dependence of on n is known exactly. For any other problem where the electron density varies throughout space, we assume that at point r is given by the homogeneous electron gas value involving the density n(r) at the same point r. This is called local density functional (LDF) theory. For high electron densities, it can be shown that is proportional to and thus in LDF theory is also proportional to . For lower densities, can still be written down but is given by a more complicated expression

AIMPRO uses LDF theory and thus the electron density is a quantity of fundamental significance.

The problem has now been reduced to a one-electron one involving the interaction of the electron with all the ions together with . Not all the electrons need be considered. Electrons are divided into two groups: core and valence electrons. The former are bound close to the ions and do not play a part in bonding. It is highly advantageous to remove these from the theory. This can be done through the use of the pseudopotential. For example, in Si the 1s, 2s, and 2p electrons are regarded as part of the core while the 3s and 3p electrons are part of the valence shell. The four bonds associated with each Si atom in the bulk arise from these four valence electrons. The pseudopotential is constructed by insisting that it has exactly the same valence energy levels as the true atomic potential, ie. the 3s and 3p and even the 3d levels are the same (the 3d levels are required because these orbitals are occupied to some extent in the solid). Moreover, the corresponding pseudo-wavefunctions are exactly equal to the true wavefunctions outside a core whose size depends on the identity of the atom. Inside the core, the pseudo-wavefunctions are not equal to the true valence ones but are very smooth nodeless functions which are easy to represent mathematically. The true 3s and 3p wavefunctions of Si oscillate inside the core and are rather difficult to represent mathematically. Fig. 1 shows these functions for Ni.

 

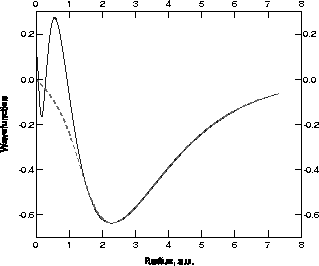
The crucial point is that the pseudopotentials have no core states at all! The lowest bound state solutions are the valence energy eigenvalues and, as stated above, these are the same as the true valence energy levels. The pseudopotential has the great virtue of making the treatment of Ge say no more difficult than carbon. AIMPRO uses the pseudopotentials due to Bachelet, Hamann and Schlüter (BHS) who have given tables for all the elements from H to Pu.

Despite these great simplifications, we are still confronted with a formidable problem. We need to solve the eigenvalue problem:

Here H includes the kinetic energy, the sum of the pseudopotentials for all the ions present, and the effective potential which depends on the density of electrons n(r). To proceed we expand the wavefunction in terms of a basis . Thus

Two choices of are often made: plane waves and Cartesian Gaussian orbitals. Using the first is equivalent to making a Fourier transform of the wavefunction. This has problems with certain elements, eg. first row, transition and rare-earth ones where the wavefunction varies rapidly and a great number of plane waves are required. AIMPRO uses Cartesian Gaussian orbitals of the form

when centred at the origin. In practice, they are centred at the nuclei and sometimes at bond centres sites between the nuclei. If then the orbitals are simply spherically symmetric Gaussian functions sometimes called s-Gaussian orbitals. If one of the is unity, and the others zero, then the functions are p-Gaussian orbitals while if the sum of the is 2, the set of six orbitals generate five d-orbitals and one s orbital. The great advantage of Gaussian orbitals is that analytical expressions can be given for all the integrals.

We now have to solve the equations

The next step is to multiple this equation through by and integrate over r. This reduces the differential equation to a set of matrix equations:

which can be solved by matrix methods. and are matrix elements of the Hamiltonian and the overlap respectively.

Once this equation has been solved we can generate the output charge density

In general this is not equal to the charge density used to generate the effective potential . Of course, this is wrong and we need to devise a scheme whereby the input charge density, which is used to construct , is equal to the output density. This is usually carried out by an iterative procedure and the process of achieving equality in the densities is called the self-consistent cycle.

AIMPRO uses an internal representation of the charge density by expanding it in a basis of s-Gaussian functions . Thus

The particular exponents of the Gaussian together with the exponents on the basis functions have been calculated for atoms and given in a single data file called bhs.lib.

Once the self-consistent density has been found, the structural energy E(R) can be evaluated. We then compute he forces on each atom from and move the atoms until this energy is a minimum and these forces vanish. This is called relaxing the assembly of atoms.

The user of AIMPRO needs to provide 1) the positions of the atoms in the cluster (in atomic units); 2) the basis to be used for the wavefunction and charge density; 3) the electronic configuration; 4) the identities of the atoms which are to be relaxed. The output gives the energy, electronic levels , and positions of the atoms. More specialised output is available.

• Up to the AIMPRO group page