
Dipole transitions


|
Dipole transitions |

|
An optical (electric dipole) transition can be forbidden by symmetry. Let us restrict the analysis to cases where a there is no change in overall symmetry between the ground and excited states. Whether an electronic transition is forbidden or not can be ascertained by examining the product of the symmetries of the ground and excited states of the possible transition. If the product contains the irreducible representation that corresponds to the dipole (x, y, and/or z), then the transition is allowed in principle.
Equivalently, if the product irreducible
representations of the ground, excited and dipole-operator contains
the totally symmetric irreducible representation, then the transition
is allowed. This selection rule can be expressed as:
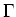 GS
GS 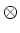
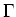 p
p 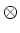
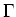 XS
XS 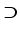
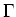 Sym
Sym
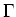 GS GS |
is the irreducible representation of the electronic ground state |
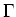 p p |
is the irreducible representation of the dipole operator |
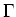 XS XS |
is the irreducible representation of the electronic excited state, and |
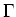 Sym Sym |
is the totally symmetric irreducible representation of the point group (usually denoted by A, A1, A1g, Ag, or A') |
For specific point groups, the direct products if irreducible
representations with those transforming as x, y, and/or
z have been tabulated. (Follow links labelled product tables
or by the  symbol.)
symbol.)
In a similar way, vibrational replicas of dipole transitions follow the selection rule:
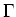 GS
GS 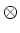
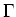 p
p 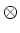
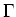 XS
XS 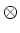
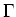 LVM
LVM 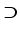
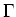 Sym
Sym
where the symbols are as before, and
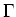 LVM is the irreducible
representation of the vibrational mode. Clearly a totally symmetric
mode of vibration is always a possible replica. To determine whether
modes transforming as other irreducible representations can couple to
the electronic transition requires application of the selection
rule.
LVM is the irreducible
representation of the vibrational mode. Clearly a totally symmetric
mode of vibration is always a possible replica. To determine whether
modes transforming as other irreducible representations can couple to
the electronic transition requires application of the selection
rule.
Fortunately this is straight forward, and the direct product tables already contain the relevant information.
Furthermore, in general the product of an irreducible
representation with itself always contains the totally symmetric
irreducible representation. Moreover, the products of non-degenerate
irreducible representations with each other (but not with themselves)
do not. These results have the consequence that the product 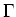 GS
GS 
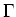 p
p 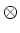
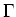 XS directly represents all group
theoretically possible modes that can couple with the electronic
excitation.
XS directly represents all group
theoretically possible modes that can couple with the electronic
excitation.
Note, dipole forbidden transitions follow the same selection rule, and consequently totally symmetric modes cannot be phonon replicas of forbidden transitions.