Diamond and Related Materials, 2(12), 1493-1499 (1993)
C. D. Latham (a), M. I. Heggie (a), R. Jones (b)
(a) Department of Computer Science, University of Exeter, Exeter, EX4 4PT, UK
(b) Department of Physics, University of Exeter, Exeter, EX4 4QL, UK
Two novel CVD diamond growth mechanisms are proposed which involve methyl radicals and acetylene molecules where carbon atoms are inserted into {100} 2×1 monohydride dimer surface reconstruction bonds. We have built models of the three principal surfaces of diamond and performed ab initio local density-based calculations to determine structures and energies of surface reactions including the two postulated for 2×1 reconstructed {100}. Both of these processes are found to be exothermic but with large barriers. However, they do demonstrate that reconstruction bonds can facilitate growth. The results are discussed with respect to the large body of recent experimental results and we conclude that the relative contributions of methyl and acetylene depend on the system used.
(Received 2nd February 1993; accepted in final form 5th February 1993)
Significant progress has been made in the understanding of the processes involved in CVD diamond growth recently though much research is still needed. The problem of there being a large number of observed experimental parameters which affect the outcome is exacerbated by the difficulty of making accurate measurements under CVD conditions.
The most certain observation is that diamond is produced. The vast number of Raman spectra and electron micrographs produced by experimentalists provide unequivocal evidence of this. At first sight this is slightly surprising as diamond is a metastable state, but is perhaps less surprising when one considers that graphite is lower in energy by only ~0.02 eV/atom [1] and there is a large barrier between the two. Graphite is either preferentially etched away or in some way converted into diamond in a CVD reactor by a mechanism which is not yet understood.
We can also be fairly certain that in some way either the methyl radical or acetylene molecule is the species responsible for growth, with the former currently emerging as the favourite and the latter not entirely excluded. Both are present in sufficient quantities with of order ten times as much acetylene as methyl but methyl being the more reactive. Much of the gas chemistry is well known and it is likely that the diamond surface has some features in common with a large hydrocarbon molecule. Beyond that though the state of current knowledge is still sketchy.
Harris et al. [2-5] have studied mechanisms for CVD diamond growth on the three principal surfaces of diamond. They perform experiments and calculations to support their view that methyl is the principal growth species. Acetylene is not ruled out entirely but it plays a lesser role and yields poorer quality material. They conclude that methyl addition occurs on the (100) surface by a mechanism which results in a C-CH2-C bridge being formed at the site they denote as HH [2] and at topologically related ledges on the (111) surface [4, 5]. They find (111) surface growth cannot be explained by simple abstraction-addition reactions without steps; it is thermodynamically unfavourable [5].
Chu, D'Evelyn, Hauge & Margrave [6-8] employ carbon-12/carbon-13 isotopic labelling to identify the growth species. They are confident that scrambling of the two isotopes does not occur and infer from the experimental results that methyl is the principal growth precursor. Again, acetylene is not excluded but does appear to have a lesser role. Johnson, Weimer and Cerio [9] estimate that the growth rate due to methyl (assumed to come from CH4) is approximately a factor of ten greater than that due to acetylene in their isotopic labelling experiment.
The effects of steric hindrance on unreconstructed 1×1 {100} surfaces are discussed by L. F. Sutcu et al. [10] who see evidence of a 2×1 {100} surface reconstruction occurring. They believe this may be a factor in the observed activation energies for diamond growth which appear to be different for different surfaces [11] though it cannot be the only factor as results from ostensibly similar experiments yield values which do not overlap within their error bounds [12].
There is still a gap between theoretical models of CVD diamond growth at an atomistic level and experiments which aim to discover the exact reaction pathways. Recent calculations can be divided broadly into two camps: many-body potential based methods and ab initio calculations. Calculations using potentials are faster, can model large numbers of atoms and include molecular dynamics without a large time penalty. There is always an element of doubt though, particularly where there are complex changes in atomic hybridization and bonding. Ab initio calculations largely remove such doubt (though one needs to be careful about what level of approximation has been used), but at greater computational expense and consequent limits on the size of problems which may be tackled.
Brenner [13] and Garrison et al. [14], have drawn on the substantial pool of experience of using empirical many-body potentials to model CVD diamond growth at an atomistic level. Their elaborate potentials are carefully tailored to match experimental data for hydrocarbons. We will make comparisons with their results later, together with the work of Pederson, Jackson & Pickett [15], who have performed impressive gradient corrected local spin density calculations. Other recent studies by Yang et al. [16-18] compare empirical molecular mechanics with experiment on {100} diamond surfaces (which they believe are mainly in the 2×1 monohydride reconstructed state under CVD conditions). Finally, semi-empirical MNDO calculations by Huang & Frenklach [19] and Deák et al. [20] demonstrate several plausible mechanisms for diamond growth.
The three principal surfaces of diamond were modelled by taking clusters of about twenty carbon atoms cut from the diamond structure and terminating surface dangling bonds with hydrogen, this being the usual state in air or under CVD conditions. The geometry of the clusters was carefully chosen to avoid having any of the saturating hydrogen atoms in uncomfortably close proximity to each other, except on hydrogenated {100} unreconstructed surfaces where steric interactions are inherent. We use an ab initio local density functional pseudopotential method with a Gaussian basis set of s- and p- orbitals [21-23] to calculate the energies and structures of the reactions studied here. Between two and six independent 2s- and 2p- Gaussians per atom were used to describe carbon wavefunctions and two or three for the hydrogen 1s-, together with a norm-conserving pseudopotential [24] for C. The Ceperley-Alder [25] expression was used for the exchange-correlation energy. Different parts of the clusters were treated with different precision, that is, different numbers of Gaussians per atom, with more at reaction sites and fewer on atoms in less critical positions. The charge density was fitted to s- like Gaussians only; two, three, four or six for C and three or four for H. Free atom values for the Gaussian exponents are not always optimal, particularly for larger clusters, where long ranged Gaussians substantially overlap leading to numerical instability. Accordingly, we made adjustments to the exponents where appropriate. In this way, by individually tailoring the basis used for a given problem, we were able to keep within the limits of numerical stability, dictated by the computer hardware, without having to give up full variational freedom over the basis. Energy minimisation of the structures was performed using a conjugate gradient algorithm and semi-analytically derived forces on the atoms. By constraining the movements of selected atoms and relaxing all others, reaction pathways could be simulated and energy barriers found.
To begin, in table 1 are the results of our calculations of binding energies of hydrogen atoms and methyl radicals to (111), (110) & (100) surfaces together with those of Brenner [13], Garrison et al. [14] and Pederson et al. [15]. Also included for the purpose of comparison are the results of our calculations for a ten carbon atom cluster, ostensibly the same as Pederson, Jackson and Pickett's, with measured values [1] for t-C4H9 + H, CH3 + H, t-C4H9 + CH3 and CH3 + CH3.
There are a number of observations to make here. Hydrogen binding energies to (111) are nearly all in the range 4-5 eV. The value calculated for (110) also lies in this range. The calculated energy for CH3 + H is a little high because our code is less well suited to problems involving small radicals -- it uses a spin averaged scheme. In our emulation of Pederson's calculation (C10H21 + H, CH3) it should be noted that there are a number of hydrogen atoms on the back of the cluster which are only ~0.6 Å apart, severely straining the structure. The larger clusters we used avoid this problem and have the advantage that all nearest and second-nearest neighbour carbon atoms to the central surface atoms are included, in addition to some third-nearest neighbours. The (100) surface is complicated by steric strain in the dihydride, unreconstructed state. This causes a 5&176; twist of the surface CH2 groups from the [110] direction and makes the binding energy for H over 0.7 eV lower than on (111) and (110). The formation of a reconstruction bond on (100) lowers the binding energy of a second H atom on the adjacent CH2 group to only 1.1 eV. The calculated length of the reconstruction bond is 1.67 Å and in connection with this, it should be noted that we obtain a diamond C-C bond length indistinguishable from the experimental figure of 1.54 Å. For the hydrogen binding energies we used the exact value for the total energy of a hydrogen atom because this case is so poorly modelled. It is likely that the reason for our methyl radical binding energies being on the low side is that the effects of spin-polarisation are still significant. The general trend is, though, that methyl is less well bound to diamond surfaces than hydrogen.
We have already seen how {100} surfaces in both the unreconstructed and reconstructed states are fundamentally different from both {111} and {110}, which only exist in topologically similar monohydride forms. The following calculations consider the special properties of {100} surfaces in more detail, starting with the transition between the dihydride and monohydride forms. A twenty-one carbon atom cluster with a (100) surface which had one pair of dihydrogenated carbon atoms in the centre, between two pairs of monohydrogenated carbons, was taken as the initial state. Intermediate structures were then generated by linear interpolation between the initial cluster and a final one where the central dihydride pair was replaced by a reconstructed monohydride dimer and a hydrogen molecule about 3 Å away. Each cluster was relaxed to minimise the total energy but constrained so that (i) the pair of hydrogen atoms which form a molecule in the final state could only move in the given (100) plane and (ii) one carbon in the diamond at a central position was held fixed. Essentially, the hydrogen molecule was pulled off the diamond surface in the [100] direction, allowing a new C-C reconstruction bond to form in the process. Figure 1 illustrates this and the corresponding energy curve obtained is plotted in figure 2. The barrier to spontaneous reconstruction is approximately 4 eV but so is the reverse, making both surface structures almost equally stable. This energetic equality of the monohydride and dihydride surfaces could be an important feature to facilitate the emission of hydrogen from the growing diamond surface. In a sense, the {100} surface could act as a buffer for hydrogen.
If we make the assumption that the hydrogen abstraction, methyl addition process occurs on a reconstructed (100) surface, then rearrangement of the methyl group must follow to get diamond. The CH3 rotates in the (110) plane to form a C-CH2-C bridge over the adjacent reconstruction bond while leaving one H behind to form a bond with the C atom where the CH3 group was formerly attached. The resultant structure is diamond. Finding a suitable way to constrain a cluster to examine the methyl group rearrangement in more detail is less obvious than for the reconstruction reaction. We chose to hold two atoms fixed for each of the intermediate structures, generated by linear interpolation, while allowing all the others to relax. The rearrangement of the methyl group is illustrated in figure 3 and the corresponding energy curve is plotted in figure 4 which gives the energy barrier to this process as 4 eV. The final structure is 1.5 eV lower in energy than the initial one. Rapid hydrogen abstraction-addition reactions occur at a very high rate over diamond surfaces under CVD conditions, so it is likely that an attached methyl group would lose a hydrogen within its lifetime. Performing a similar rearrangement with a CH2 group in place of the CH3 (leaving a dangling bond on the end carbon) reduces the activation energy to 1.8 eV, but the energy difference between the initial and final states becomes less favourable at 0.8 eV. The energy curve has the same shape; the amplitude, however, is smaller.
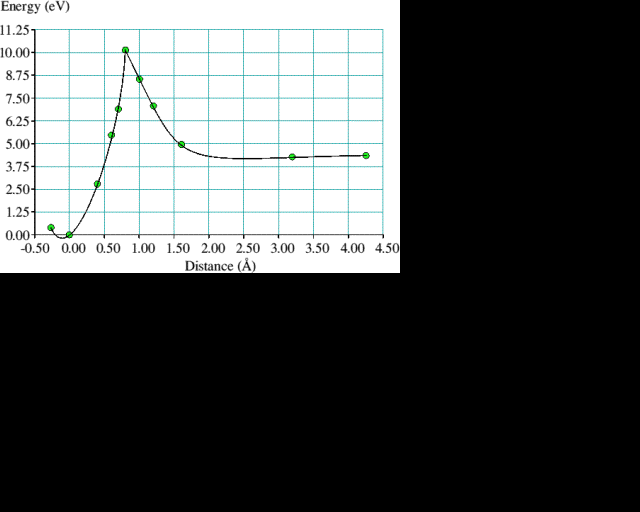
Reconstruction bonds on {100} monohydride surfaces may also be attacked by acetylene without hydrogen removal. We show, illustrated by figure 5, that an acetylene molecule approaching a pair of (100) reconstruction bonds on a dimer row, with sufficient energy, could break the bonds while simultaneously forming four new C-C bonds and transforming the acetylene triple bond into a single reconstruction bond. In this reaction there is a smooth transition between the starting and final structures as the acetylene molecule forces itself between a pair of reconstruction bonds. Intermediate structures for the energy barrier calculations were derived in the same manner as before by linear interpolation and the atoms were constrained in a similar fashion to that used for the (100) reconstruction reaction. On this occasion it was the two acetylene C atoms which were allowed to move in the given (100) plane only, while holding a central C in the diamond fixed. The acetylene molecule's H atoms move progressively from a linear arrangement to one with their bonds pointing away from the surface. In the energy curve for this reaction, plotted in figure 6, we see that the peak of the barrier occurs when the acetylene molecule is approximately 1 Å from the surface and is some 6 eV in height. Closer than 1 Å the energy falls precipitously to 4 eV below the unbound, separated value, so an activation energy of 10 eV would be required to reverse the reaction.
The 6 eV barrier to the proposed acetylene reaction may not give an entirely accurate picture of what happens in reality. It is entirely conceivable that a molecule randomly impinging on the surface is caught in a reconstruction bond at one end then, carried round by its momentum, rotates and is captured in the neighbouring reconstruction bond at the other end. A two step process such as this might have lower energy barriers than the symmetrical case, but with so many possible paths it would be difficult to identify unambiguously the optimum reaction coordinate. The sharp energy peaks in the the energy curve plots are a consequence of our approximation to the reaction coordinate. The ideal method would be to calculate the energy Hessian and find a saddle point structure for which one eigenvector has eigenvalue zero. Currently, we do not have the computing resources to perform such a task.
Reviewing experimental probes of the growth species, an acknowledged criticism of all the experiments to date which point to the methyl radical as having the central role in the growth process are of the low pressure, slow rate variety [26]. The methyl radical may well predominate under these conditions but not necessarily under other growth regimes. In connection with this, it is interesting that growth rates up to a thousand times higher than can be achieved with the low pressure methods, have been obtained using modest, inexpensive equipment, namely oxyacetylene flame CVD and dc plasma jet CVD [27]. As yet there is no clear explanation why oxyacetylene flame and dc plasma jet CVD are more successful. Experimental probes for the more extreme conditions are difficult, if not impossible to devise. Improved transport has been proposed as a likely candidate [26], but it may be that the predominant growth mechanism itself is different too. Intuitively, one would expect this to be the case for oxyacetylene flame CVD where a very large flux of acetylene molecules is directed at a substrate and this is what motivated the present study.
Although our novel acetylene growth model concentrates on {100} it still has a bearing on {111} growth. Similar reconstruction type bonds may occur at surface ledges on {111} surfaces which are in effect long, narrow {100} like facets. There are two possible orientations of the bonds; one parallel with a step lying along the <110> direction and the other perpendicular to the step direction. Acetylene can only add on in the manner described above when the reconstruction bonds are in the perpendicular direction but the methyl rearrangement mechanism works for both types of step. {110} surfaces do not have the right geometry for creating ledges of this type which may explain why in the first instance this orientation is not often seen in CVD diamond and secondly, why where it does occur, it is very rough. So far the question as to what happens between the dimer rows has not yet been considered. Both the methyl and the acetylene mechanisms insert carbon atoms into reconstruction bonds, pushing apart the reconstruction pairs in the process. This will in turn move pairs of hydrogen atoms on neighbouring rows closer so reconstruction can then occur here by hydrogen abstraction or desorption, hence completing the cycle and generating a new (100) surface. The process of filling the valleys between the former dimer rows will probably be slightly modified by the fact that there is now a surrounding structure which will have to deform a small amount to accommodate the strain caused by the reconstruction bonds.
Garrison et al. [14] consider very similar dimer opening mechanisms. However, they obtain different results with their many-body empirical potential molecular dynamics method. The CH3 rearrangement is not observed in their simulations and the energies for the CH2 insertion into a reconstruction bond (table 2) are lower than ours: they have only -0.20 eV for the difference between the initial and final states. This is over 0.5 eV smaller in magnitude than the ab initio result. Furthermore, they find an activation energy of only +0.2 eV, far lower than our +1.8 eV. Huang and Frenklach [19] also calculate a barrier height and energy for the CH2 reaction but their MNDO-based result does not agree with either ours or Garrison's. They obtain +2.39 eV and +0.19 eV respectively (that is endothermic). In summary, we believe the poor agreement between theory values undermines the fragile foundations of the empirical methods rather more than the more robust ab initio method used here.
We can reinforce this point by comparison with other calculations and experiment for the desorption of hydrogen molecules from {100}. The semi-empirical MNDO method used by Huang and Frenklach gives 1.61 eV for the barrier to H2 desorption from a (100) 1×1 surface and they find the monohydride reconstructed surface is 3.44 eV per 2×1 reconstruction dimer lower in energy than the dihydride unreconstructed one. Yang et al. [16-18] predict that the reconstructed surface is lower in energy too, this time by 2.13 eV, but admit the shortcomings of their empirical MM3 method: the bonds between atoms on diamond {100} surfaces are strained outside the regime where the theory has been demonstrated to be valid. In this context it should be noted that the length we obtain for the reconstruction bond (1.67 Å) is slightly greater than both MNDO (1.64 Å) and MM3 (1.63 Å) give. It appears to us that there could be few artificial reasons for this long bond arising from our calculation, since we have a small molecule with no external (elastic) constraints. On the other hand, it is easy to see how an empirical method would always try to force a diamond-like bond length here. The situation is summarised by table 3. It is apparent from the wide scatter of values that empirical and semi-empirical methods are not able to model these reactions accurately. Indeed, the results of earlier work by Verwoerd [28] and Mehandru and Anderson [29] further serve to emphasise the poor quantitative agreement among semi-empirical calculations. Interestingly, Yang et al. also measure by a temperature programmed desorption experiment an activation energy for H2 emission from diamond {100} [18]. It is estimated to be ~3.5 eV but they argue the hydrogen is desorbed from monohydride surfaces, as favoured by their calculation. Given the difficulty of the experiment this value lies remarkably close to our calculated figure of 4 eV for desorption of H2 from the dihydride surface. This observation combined with the one that both the 1×1 and 2×1 forms exist, is indicative to us of there being no more than a small difference in formation energies between them and a significant energy barrier. An ab initio calculation for H2 desorption from the 2×1 {100} reconstructed surface will certainly be needed to resolve the matter properly. For the present though, the proximity of the experimental and ab initio results invites speculation as to whether H2 desorption from the dihydride rather than the monohydride was in fact observed.
We have presented models for diamond film growth based on addition of methyl radicals and acetylene molecules to the three principal surfaces of diamond including the associated step of hydrogen abstraction. In agreement with experimental observation, our models are essentially irreversible reactions. We explain the special properties of {100} surfaces and the closely related <110> steps on {111} surfaces. Steric interactions on unreconstructed {100} surfaces significantly reduce the energy required to remove a single hydrogen atom and the energy needed to remove a second, adjacent hydrogen is lowered still further by the subsequent 2×1 surface reconstruction. We have shown that the reconstruction bond on {100}, which is rather weaker than a strong carbon sp³ bond, provides a vulnerable point to facilitate growth and we have examined detailed mechanisms by which this might occur. In addition, the near equality in formation energies which we predict for the mono and dihydride {100} surface states possibly make {100} surfaces a buffer for hydrogen in the system. Our models demonstrate how hydrogen abstraction by atomic hydrogen from an attached CH3 group on a 2×1 (100) surface, converting it to CH2, reduces the energy barrier to the transformation of the structure into diamond. Mechanisms involving methyl radicals have lower activation energies than the model acetylene reaction, but we propose that acetylene, with the statistical advantages of higher concentration than methyl and of not needing to encounter a surface dangling bond, could be important in CVD methods which are sufficiently energetic to overcome the large barrier.
This work has been carried out with the support of the DRA Malvern.
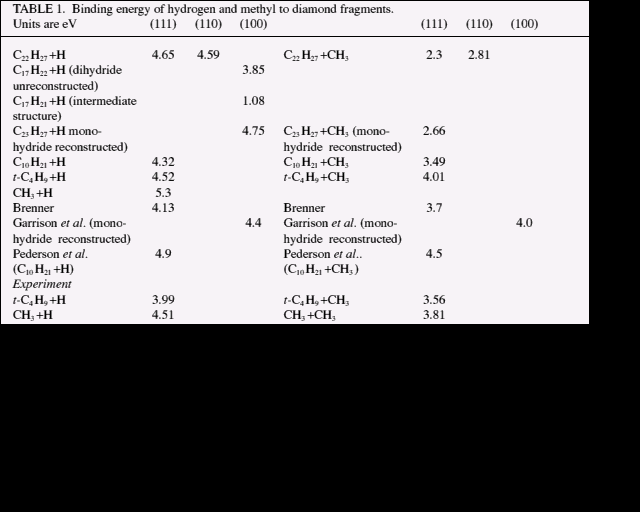
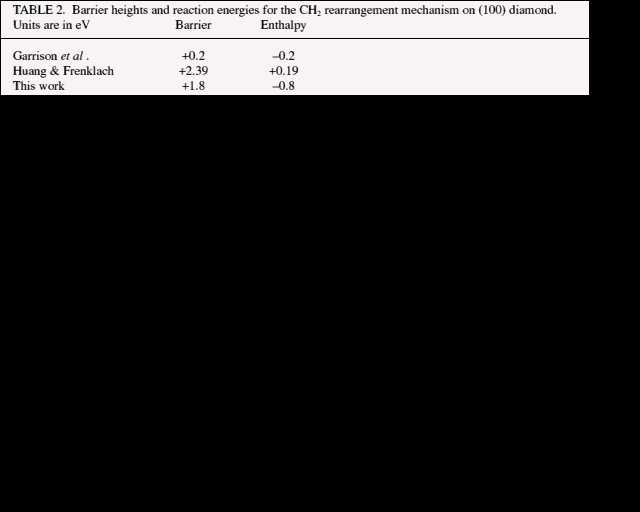

Figure 1. Formation of a reconstruction bond on a hydrogenated diamond fragment with (100) surface by the elimination of a hydrogen molecule; (left) unreconstructed, (centre) intermediate and (right) reconstructed. To obtain the energy curve in figure 2, the shaded carbon atom was held fixed and the hydrogen pair was restricted to movement in the (100) plane only. All other atoms were free to move. Hydrogen atoms are represented by the smaller circles, carbon ones by the larger.

Figure 2. The corresponding energy curve for the process illustrated in figure 1. The solid line joining the calculated points is drawn only to guide the eye.
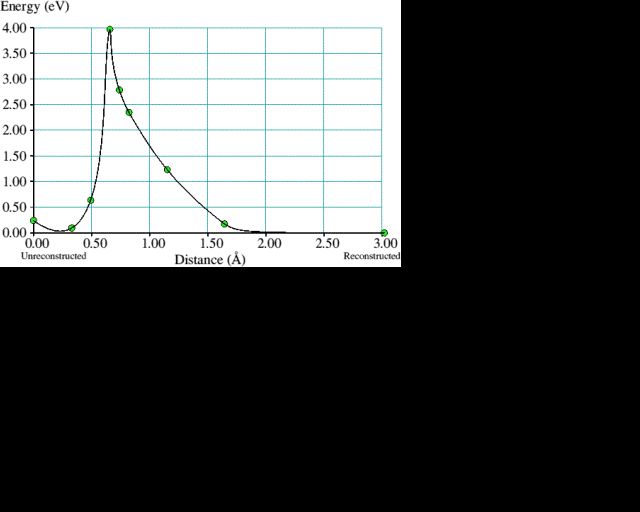
Figure 3. Rotation of a methyl radical bonded to a (100) 2×1 reconstructed diamond surface into the reconstruction bond; (left) initial state, (centre) intermediate and (right) final state. The two fixed carbon atoms are shaded, while all others were allowed to relax.
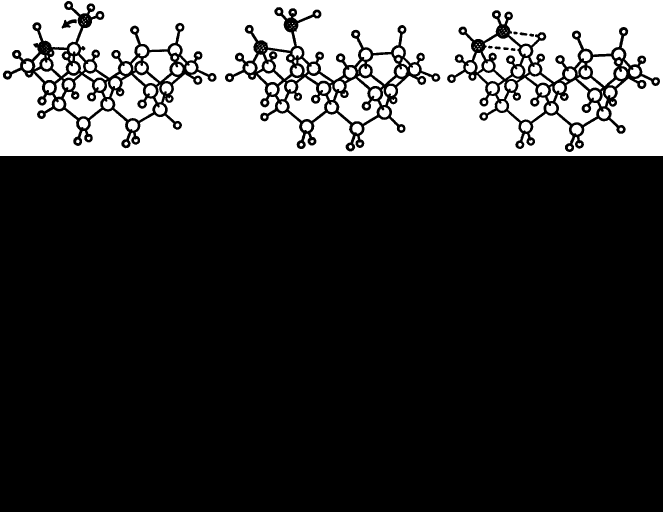
Figure 4. The corresponding energy curve for the process illustrated in figure 3. Note the reaction coordinate from initial to final state in figure 3 goes from right to left. The solid line joining the calculated points is drawn only to guide the eye.
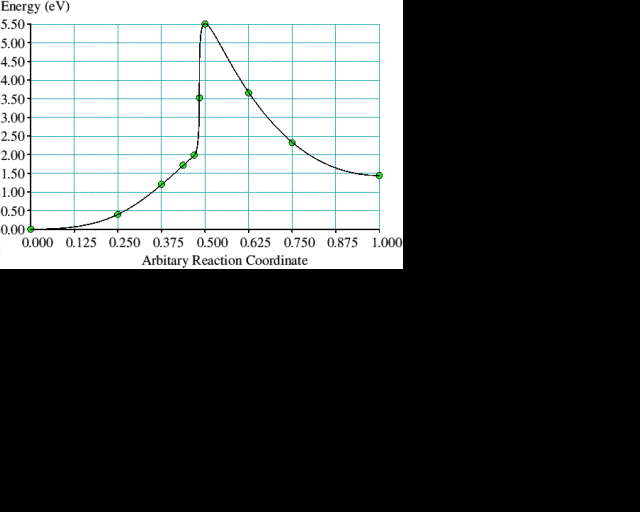
Figure 5. Insertion of an acetylene molecule into a pair of (100) reconstruction bonds. The central carbon atom of the diamond cluster was fixed and the two acetylene carbons were constrained to the (100) plane.
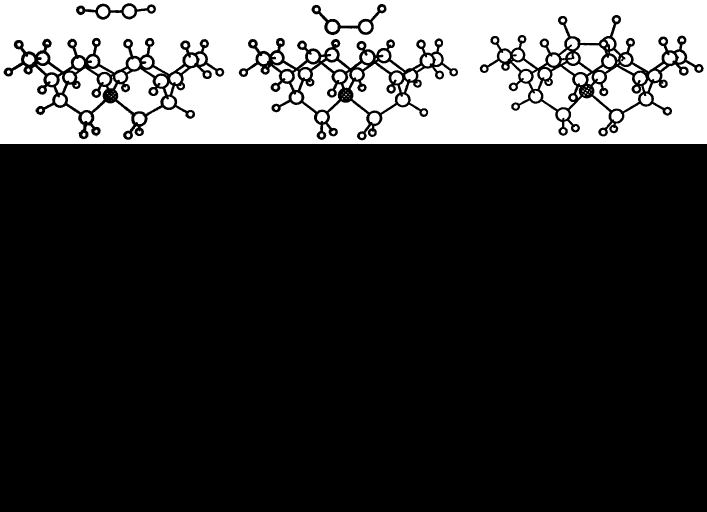
Figure 6. The corresponding energy curve for the process illustrated in figure 5. The solid line joining the calculated points is drawn only to guide the eye.
| Christopher D. Latham | HTML 3.2: [W3C][WDG] |